

სხვა როგორ ვასწავლოთ გონებაში დათვლა ბავშვს 2020, 12 მარტი, 15:17  ბავშვებს სკოლაში საკმაოდ უჭირთ: ან რაღაც ავიწყდებათ, ან საშინაო დავალებაა ბევრი. და როდესაც საქმე მათემატიკის შესწავლამდე მიდის, უმრავლესობამ საერთოდ არ იცის პირველ რიგში რა უნდა აითვისოს და როგორ იმუშაოს რთული ციფრებით, ფორმულებით და სხვა თავსატეხებით. არსებობს რამდენიმე ხრიკი, რომლებსაც შეუძლიათ ოდნავ მაინც გაუმარტივოს ცხოვრება ნებისმიერ მოსწავლეს, განსაკუთრებით მაშინ, თუ გაკვეთილზე კალკულატორის გამოყენებას კრძლავენ. სწორედ მათზე მოგითხრობთ ახლა. 1. იმ რიცხვის კვადრატში აყვანა, რომელიც მთავრდება 5-ზენებისმიერი ორნიშნა რიცხვი, რომელიც მთავრდება 5-ზე, იოლად ასაყვანია კვადრატში, საჭიროა მხოლოდ რიცხვის პირველი ციფრი (ათეული) გაამრავლოთ ციფრზე, რომელიც მეტია ერთით. შემდეგ კი მიღებულ მნიშვნელობას მიაწეროთ 25. მაგალითად კვადრატში უნდა ავიყვანოთ 65: პირველი ნაბიჯი: 6 Х 7 = 42. მეორე ნაბიჯი: მივუწეროთ 25, მივიღებთ 4225. 2. ორნიშნა რიცხვების კვადრატში აყვანართული ორნიშნა რიცხვის კვადრატის გამოთვლაც ძალიან იოლია, თუ ის მთავრდება 1-ზე. საჭიროა საწყისზე ერთით ნაკლები რიცხვის კვადრატს მივუმატოთ ესავე ერთით ნაკლები რიცხვი და საწყისი რიცხვიც.
მაგალითად, საჭიროა ვიპოვოთ 41-ის კვადრატი: 41^2 = 40^2 + 40 + 41 = 1 600 + 81 = 1 681.3. ორნიშნა რიცხვების გამრავლება 11-ზეიმისათვის, რომ ორნიშნა რიცხვი სწრაფად გავამრავლოთ 11-ზე, საჭიროა შევკრიბოთ ეს რიცხვები. თუ ჯამი გამოდის ერთნიშნა, მაშინ მას უბრალოდ ჩავსვავთ საწყისი რიცხვის შუაში. მაგალითად, 63 х 11 = 693 (9 = 3 + 6). 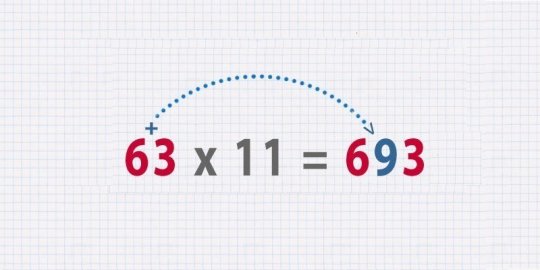
თუ ჯამი გამოდის ორნიშნა, მაშინ ალგორითმი რთულდება ერთი ნაბიჯით. ჯამის ბოლო ციფრს ასევე ვსვავთ საწყისი რიცხვის შუაში, ხოლო ჯამის პირველი რიცხვი- ყოველთვის ერთიანია, იმდენად რამდენადაც ორი რიცხვის ჯამი ვერასოდეს იქნება 18 (9+9)-ზე მეტი. და ამ ეთიანს უბრალოდ მივუმატებთ საწყისი რიცხვის პირველ ციფრს. მაგალითად: 93 х 11 = 9(12)3 = 1 023.4. რთული გამრავლებაზოგ შემთხვევაში რიცხვების ერთმანეთზე გადამრავლებაში გვეხმარება მათი დაშლა მარტივ მამრავლებად. მაგალითად, 16 х 225 = (2 х 2 х 2 х 2) х 225 შემდეგ თითოეულ ორიანს ცალცალკე ვამრავლებთ გასამრავლებელ რიცხვზე და შედეგის პოვნაც არც თუ ისე რთული გამოდის. (2 х 2 х 2) х (2 х 225) = (2 х 2) х (2 х 450) = 2 х (2 х 900) = 2 х 1 800 = 3 600. 5. ერთიანებისგან შემდგარი რიცხვების თავის თავზე გამრავლებაამ კანონზომიერების სიტყვებით ახსნაზე უფრო მარტივია ამ ცხრილის დაკვირვება. მთავარია - სწორად დათვალოთ ერთიანების რაოდენობა რიცხვში.
 6. სამნიშნა რიცხვების გამრავლება ერთნიშნაზე ყველაფერი გენიალური მარტივია, საჭიროა მხოლოდ „საშინელი“ სამნიშნა რიცხვი დავშალოთ მარტივებად. მაგალითად, 284 х 3 = (200 + 80 + 4) х 3 = (200 х 3) + (80 х 3) + (4 х 3) = 600 + 240 + 12 = 852. 7. როგორ მოვძებნოთ დიდი რიცხვიდან პროცენტიამოცანის გასამარტივებლად რიცხვსაც და პროცენტსაც ვყოფთ 10-ზე, შემდეგ კი შედეგებს ვამრავლებთ ერთმანეთზე. მაგალითად, 300-ის 70 %: 7 х 30 = 210. 8. 9-ის გამრავლების ცხრილითუ გვიჭირს დაზეპირება, დაგვეხმარება ხელები. ვუყურებთ ხელებს და ვხრით თითს, რომელიც შეესატყვისება გასამრავლებელ რიცხვს. მის წინ თითების რაოდენობა - ათეულებია, მის შემდეგი კი - გამრავლების შედეგად მიღებული ერთეულები.
მაგალითად, 6 х 9 = 54 ( 5 თითი მოხრილამდე და 4 მოხრილის შემდეგ). 
9. 5-ზე გაყოფასწრაფად და მარტივად რომ გავყოთ დიდი რიცხვი 5-ზე, საჭიროა გავამრავლოთ ის 2-ზე და მძიმით „გადავწიოთ“ ბოლო ნიშანი. მაგალითად: გვსურს 341 გავყოთ 5-ზე. ვამრავლებთ 341 -ს 2-ზე და ვღებულობთ 682-ს. მძიმეთი გამოვყოფთ ბოლო ციფრს და მივიღეთ 68, 2.
 10. მაგიური რიცხვი 1 089და ბოლოს, ეს არა იმდენად ხრიკია, რამდენადაც ინტენსიური კანონზომიერება, რომელსაც კედევ ერთხელ შეუძლია დააინტერესოს ბავშვი მათემატიკით.
უნდა ავიღოთ ნებისმიერი სამნიშნა რიცხვი, რომელიც კლებადი ციფრებით შედგება (მაგალითად 431 ან 863) და გამოვაკლოთ რიცხვი, რომელიც დაწერილია იგივე ციფრებით მაგრამ შებრუნებული თანმიმდევრობით. შემდეგ, მიღებულ სხვაობას უნდა მივამატოთ უკუღმა ჩაწერილი რიცხვი. მიღებული ჯამი ყოველთვის იქნება 1 089. შევამოწმოთ ამ მაგალითზე: 431 – 134 = 297. მიღებულ სხვაობას მივუმატოთ მისი "სარკისებური" მნიშვნელობა: 297 + 792 = 1 089.
მეორე მაგალითი: 863 – 368 = 495. 495 + 594 = 1 089. და ასე შეიძლება გააგრძელოთდაუსრულებლად, შედგი ყოველთვის იქნება 1089. 
აი ასე, რამოდენიმე ხრიკის ცოდნის გამო მათემატიკა საყვარელ საგნად შეიძლება გადაიქცეს არა მარტო ბავშვისთვის, უფროსებისთვისაც კი. სკოლაში სწავლება უფრო მარტივი და სახალისო იქნებოდა, ასეთ კანონზომიერებებს გაკვეთილებზე რომ აჩვენებდნენ და უხსნიდნენ ბავშვებს. განა ტყუილად უწოდებენ მათემატიკას მეცნერებების დედოფალს. მასში დამალულია უამრავი საოცარი, მაგრამ სრულიად ლოგიკური ფაქტები.
იხილეთ ასევე:ადამიანები ძალიან ცდებიან, როცა მსოფლიო ფასეულობად მიიჩნევენ მაგალითად ოქროს ან ნავთობს. სინამდვილეში_ ეს გონებაა. გონების და ინტელექტის გარეშე ყველანაირი სიმდიდრე კარგავს თავის ფასს. ამიტომ, ყველა ერის ნამდვილი ფასეულობა, ახალგაზრდების ინტელექტუალური შესაძლებლობებია. მოგითხრობთ ბავშვებზე, რომლებმაც თავიანთი გამოცანები უყვართ არა მხოლოდ ბავშვებს _ მაგრამ ბევრს ეს ავიწყდება. თქვენს ყურადღებას მივაქცევ 15 თავსატეხ ამოცანას. მე რამდენიმე მათგანი ვერ ამოვხსენი, და როცა პასუხები ვნახე, შოკში ჩავვარდი ყველაფერი ძალიან მარტივი ყოფილა. (იფიქრეთ... და არ ჩაიხედოთ პასუხებში თავიდანვე.) 1. მდინარესთან მიდის ორი ადამიანი. ნაპირთან ნავია, რომელსაც მხოლოდ ერთის გადაყვ... ცოლი: სად ხარ? ქმარი: სახლში, ძვირფასო. ცოლი: დარწმუნებული ხარ? ქმარი: რა თქმა უნდა. ცოლი: აბა, ჩართე მიქსერი. ქმარი: რრრრრრრრ... ცოლი: კარგი საყვარელო. მომდევნო დღეს: ცოლი: სად ხარ? ქმარი: სახლში ძვირფასო. ცოლი: ნამდვილად სახლში ხარ? ქმარი: რა თქმა უნდა ძვირფასო. ცოლი: ჩართე მიქსერი. ქმარი: რრრრრრრრრ... ცოლი: ზოგიერთ შემთხვევებში ადამიანის თვალს არ შესწევს უნარი გადაამუშაოს ინფორმაცია და სწორედ ამ დროს წარმოიქმნება ოპტიკური ილუზია. მსგავსი მოვლენის ყველაზე საინტერესო მაგალითების რიცხვშია- ეგრეთწოდებული ჰერმანის ბადე. ჯერ კიდევ 1879 წელს გერმანელმა ფიზიოლოგმა ლიუდიმარ ჰერმანმა აღმოაჩინა მოციმციმე ბადის ოპტიკური ილუზია : თეთრი ხაზების გადაკვეთაზე მუქი წე... 816 3-ს მოსწონს
|